Floating Point
정수형 표현이 아닌, 실수형 표현을 컴퓨터는 어떻게 하는지 알아보자.
실수형 표현은 정수와는 달리, 매우 크거나 매우 작은 수를 표현해야 한다. 그에 따른 규칙들이 존재한다.
normalized
- 소수점 앞의 수는 1자리 수여야 한다.
- 소수점 바로 앞 1자리 수는 1~9사이의 값이어야 한다.
- 뒤에 곱해지는 형태는 지수형태여야 한다.
ex)
-2.34 * 10^56 => normalized
+987.02 * 10^9 => not normalized (소수점 앞 수가 3자리이기 때문)
+0.0002 * 10^-4 => not normalized (소수점 앞 수가 0이기 때문)
Floating 수를 표현하기 위해서 지수부분은 소수점 기준으로 양수, 음수가 나뉘게 된다.

ex)
10.1010two = 1*2^1 + 1*2^(-1) + 1*2^(-3) = 2.625ten

55.66이라는 10진수를 표현할 때 수많은 방법이 존재한다.
5.566*10, 0.5566*10^2, 0.05566*10^3 ....... 등등등
그래서 Normalized 형태를 지정해서 사용한다.
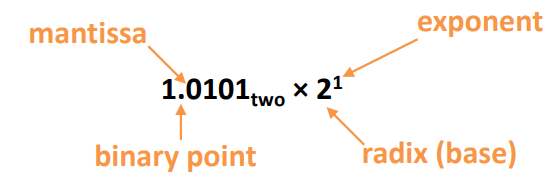
2진수도 마찬가지로 지정된 형태를 사용한다.
22라는 10진수를 Normalized 형태의 2진수로 바꿔보자.
22ten = 10110two
형태를 지키기 위해 4번 shift left 해줘야 한다.
=> 1.001two * 2^4
Floating Point Standard는 IEEE Std 754-1985에 정의되어 있다.
https://en.wikipedia.org/wiki/IEEE_754
Floating Point Encoding
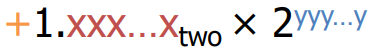

32bits의 word는 3필드로 나누어져 있다.
S는 부호 비트이고,
Exponent는 지수부분이고,
Mantissa (fraction)은 가수부분이다.
- 만약 64bits의 word였다면??
S는 1bit, Exponent는 11bits, Mantissa는 52bits로 나눠진다.
Exponent Field
Exponent field의 범위는 -127(0000 0000two) ~ 128(1111 1111two) 이다. 여기서 알아야 할 것은 0000 0000two가 원래 0이었지만, 여기서는 0이 아니다.
Exponent 0은 0111 1111two, 즉 127ten으로 나타내어진다.
ex)
2^1 이라는 수에서,
exp는 1이다. (지수부분)
exp = 1은 128을 나타낸다. ( 0111 1111two(127) + 1 => 1000 0000two )
-> (0111 1111two는 Exponent에서 0이다.)
따라서, 2^1 = 1000 0000two 로 나타낼 수 있다.
ex2)
2^127
exp = 127 => 127(0) + 127 = 254 => 1111 1110two
2^127 = 1111 1110two
그렇다면 왜 이렇게 정했을까???
예시를 하나 보자.

원래대로라면, 위 그림과 같이 표기될 것이다.
하지만! 컴퓨터는 큰 수를 판단하기 위해 왼쪽 비트부터 읽어서 1이 먼저 나오면 큰 수라고 판단한다.
그래서 -1이 1보다 더 크다고 판단해버리는 것이다.
문제를 해결하기 위한 방법이 biased notation(127의 bias(아까 했던 방법))이 사용되었다.
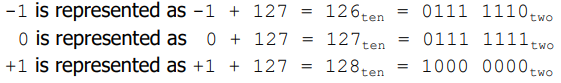
이제 컴퓨터에서 어떻게 인지하는지 살펴보자.

2003.0을 예시로 들어보자.
2003.0 = 0111 1101 0011two
-> (-1)^0 * 1.1111010011 * 2^10
S = 0
Exp = E + bias = 10 + 127 = 137 = 1000 1001two
M = 1111010011 = 111 1010 0110 0000 0000 0000two (23bit이기 때문에 나머지는 0으로 채움)
따라서 2003.0 = 0100 0100 1111 1010 0110 0000 0000 0000two 라고 표현한다.
컴퓨터는 이를 0x44FA 6000 으로 읽는다고 한다. (참고만...)
Precision and Accuracy
Precision : 얼마나 많은 bits를 사용해서 값을 표현할 것이냐.
Accuracy : 실제 표현하려는 값과 컴퓨터가 표현한 값의 차이가 적을수록 Accuracy를 높다고 표현한다.
Precision이 높을수록 Accuracy가 높아질 것 같지만, 전부 그렇지 않음.
한 예시로 파이(Pi)가 있다.
Pi는 무한소수이기 때문에 많은 bits로 표현해서 Precision이 높아지더라도 Accuracy가 따라서 높아지지 않을 것이다.
Special Case
Special Case #1 : Zero
0의 경우에는
Exp와 Mantissa가 0이면은 0이라 판단한다.
Special Case #2 : Very Small Numbers (0에 가까운 수)
a = 1.0...00two * 2^(1-127) = (1+0) * 2^(-126) = 2^(-126)
b = 1.0...01two * 2^(1-127) = (1+2^(-23)) * 2^(-126) = 2^(-126) + 2^(-149)

위 그림과 같이 Gap이 생기게 된다.
0 ~ a : 2^(-126)
a ~ b : 2^(-149)
가수부의 값을 최대한 작게 하자! => 0.0....01 => 이러면 normalized 형태가 아님...
그렇다면 denormalized 수로 표현하자!
Denorm Numbers
1이 없어도 된다.
Exp에서 Denorm exponent bias는 126에 있다는 것을 주의하자. = 0x00 (floating point가 shift left 1 bit해서)
결론적으로,
Smallest denorm: ±0.0...01two * 2^(-126) = ±2^(-149)
Smallest norm: ±1.0...0two * 2^(-126) = ±2^(-126)
Denorm Number 를 지정해줌으로써 0에 매우 근접할 수 있었다.
Special Cases #other
Exp = 0xFF, Mantissa = 0
=> ±∞
=> 0으로 나눌 때 ±∞로 갈 수 있다고 정의함.
Exp = 0xFF, Mantissa != 0
=> Not a Number (Nan) (음수의 제곱근. 허수)
정리

Convert FP to Decimal
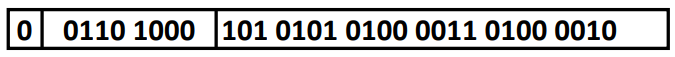
Sign : 0
Exp :
0110 1000two = 104ten
104 - 127 = -23
Bias adjustment : -23
Mantissa :
1.0101010100001101000010
= 1 + 1*2^(-1) + 1*2^(-3) + ......
= 1.0 + 0.666115
따라서 결과는, 1.666115 * 2^(-23) 이 나온다.
Convert to FP
1/3 을 나타내보자.
1/3 = 0.33333...ten
= 0.25 + 0.0625 + 0.015625 + ...
= 1/4 + 1/16 + 1/64 + ...
= 2^(-2) + 2^(-4) + 2^(-6) + ...
= 0.0101010101...two * 2^0
= 1.0101010101...two * 2^(-2)
Sign : 0
Exp : -2 + 127 = 125 = 01111101two
Mantissa = 0101010101...two
따라서 결과는, 0 | 0111 1101 | 010 1010 1010 1010 1010 1010 | 가 나온다.
결론
FP Adder 는 integer Adder보다 연산이 훨씬 복잡하다. 한 clock cycle이 너무 길다.
나중에 cycles을 쪼개서 pipeline에서 처리하는 것을 배울 것이다.
[참고]
Computer Organization and Design 5th Edition. The Hardware/Software Interface / 저자 : David A. Patterson, John L. Hennessy / 출판 : ELSEVIER
'IT > 컴퓨터구조' 카테고리의 다른 글
| [ 컴퓨터구조 ] MIPS Design Principles (0) | 2020.10.22 |
|---|---|
| [ 컴퓨터구조 ] MIPS Instructions (+Instruction to binary) (3) | 2020.10.22 |
| [ 컴퓨터구조 ] ISA (Instruction Set Architecture) (0) | 2020.09.01 |
| [ 컴퓨터구조 ] 피연산자 (Operands of Computer Hardware) (1) | 2020.05.01 |
| [ 컴퓨터 구조 ] 하드웨어 연산 (Operation of Computer Hardware) (0) | 2020.05.01 |




댓글