Perspective Projection
Perspective Projection
원근법으로 멀리 있는 건 작게, 가까이 있는 건 크게 그리는 방법이다.
Projection Matrix

만약 z의 위치에 어떤 물체가 있고, 이를 View plane에 크기에 맞춰 그리려면 닮은 비를 이용하자.
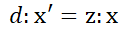
이를 x', y', z' 으로 풀어보면

이를 행렬로 표현하면 다음과 같다.


한 예시인데, 이같은 행렬 형태로 쓰인다는 것만 알고 있자.
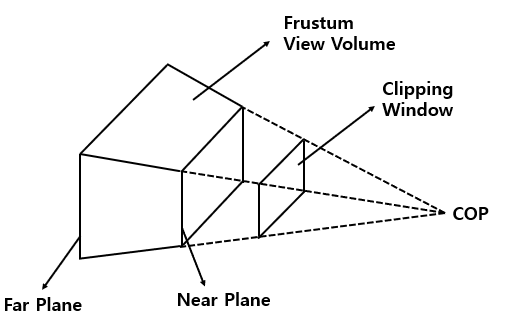
Frustum View Volume -> Normalized View Volume
Normalized Coordinates를 사용하기 위해 우선 Znear Plane과 Zfar Plane을 두고, Znear 와 Zfar를 -1 과 1 로 만들어줘야 한다.


Z 를 -1~1 로 만들어주는 Projection matrix이다.
이 matrix에 4번째 행에 -1이 있는 이유는 계산하려는 Z의 영역이 nagative 영역이기 때문이다.
Z를 -1~1로 만들어주었다.
Z를 -1~1 까지 만들었으면 이제 위아래도 똑같이 해줘야 한다.
즉 Clipping Window의 넓이도 -1~1로, 높이도 -1~1로 만들어주어야 한다.

왼쪽 Frustum View Volume에서 Perspective Mapping을 통해 오른쪽의 Parallelepiped View Volume을 만들었다고 하자.

그리고 Parallelepiped View Volume 을 Normalized View Volume 으로 만들어야 하는데,
(xwmin, ywmin, znear) 를 (-1, -1, -1) 로 만들고,
(xwmax, ywmax, zfar) 를 (1, 1, 1) 로 만드는 작업이다.

그래서 Z를 -1~1로 만들고, C와 D만큼 이동하여 화면의 Center에 맞춰주고, X와 Y도 -1~1로 만드는 Matrix는 이와 같이 나오게 된다.
OpenGL
glm::perspective(float fovy, float aspect, float near, float far)
(fovy 는 radian 단위임)

OpenGL 에서는 field of view Y (fovy) 라는 각도로 화면의 높이와 넓이를 구하게 됨.
mat4 projectionMatrix = glm::perspective 의 계산은 다음과 같이 이루어진다.
fH = tan(fovy/2) * near
fW = fH * aspect
projectionMatrix = glm::frustum(-fW,fW, -fH, fH, near, far)
(참고)
glm::frustum(left, right, bottom, top, near, far)
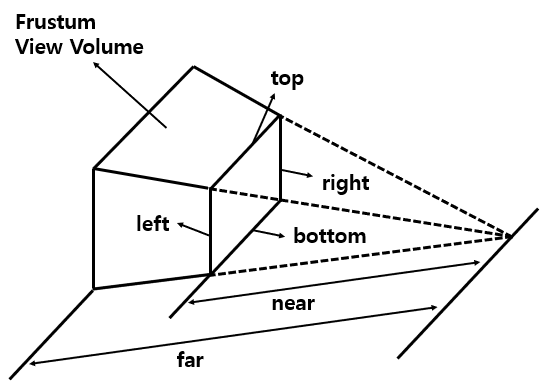
결과적으로 Frustum View Volume을 Normalized View Volume으로 만드는 Matrix 를 얻을 수 있다.
[참고]
Interactive Computer Graphics: A Top-Down Approach with Shader-based OpenGL 6th edition / 저자: Edward Angel, Dave Shreiner / 출판사: Pearson Education
'IT > 컴퓨터 그래픽스' 카테고리의 다른 글
| Aliasing과 Anti-Aliasing (1) | 2021.02.03 |
|---|---|
| Rasterization (0) | 2021.01.31 |
| Camera Coordinates (0) | 2021.01.17 |
| GPU와 Buffer (0) | 2021.01.17 |
| GPU에 data를 전달하기 (0) | 2021.01.17 |




댓글