임의의 축으로 회전하기
3D 환경에서 x축, y축, z축으로 회전하는 건 4X4 matrix로 할 수 있다.
그러면 임의의 축으로 회전하는 건 어떻게 할까?
순서
1. 임의의 축이 좌표축과 평행할 때 (Special Case) 회전
2. 좌표축과 평행하지 않은 임의의 축 회전
- 5 Step이 있음
- α와 β를 구하는 법
- 다른 형태의 matrix
임의의 축이 좌표축과 평행할 때 (Special Case)
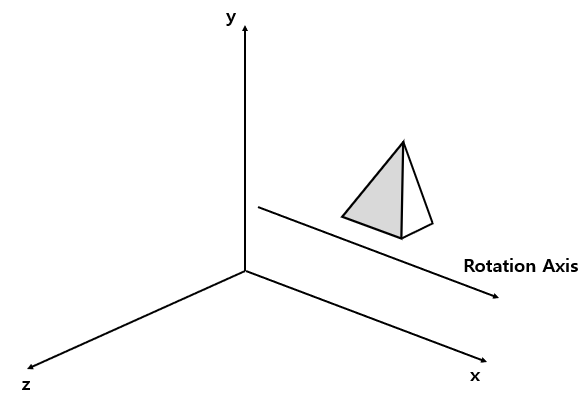
임의의 축이 x과 평행하다고 해보자. 이럴 때 회전은 어떻게 될까?
다음과 같이 진행된다.
1. 임의의 축을 x축으로 이동
2. x축 기준으로 회전
3. 임의의 축을 원래 자리로 이동

1. 임의의 축을 x축으로 이동

2. x축 기준으로 회전

3. 임의의 축을 원래 자리로 이동
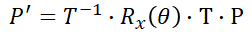
회전하는 점의 식은 이와 같다.
x축으로 이동하고, x축으로 회전하고, 원래 자리로 이동하는 것이다.

Rotation matrix는 이렇게 구할 수 있다.
이것도 x축으로 이동하고, x축으로 회전하고, 원래 자리로 이동하는 matrix를 연산한 것이다.
임의의 축 기준으로 회전

이번엔 어떤 축과도 평행하지 않은 정말 임의의 축을 기준으로 회전해보자.
어떻게 회전할까?
순서는 이와 같다.
Step 1. P1 점을 원점으로 이동
Step 2. 좌표축을 z 축에 맞게 회전 <= (여기에 주목)
Step 3. z축 기준으로 회전
Step 4. 원래 상태로 회전
Step 5. 원래 자리로 이동

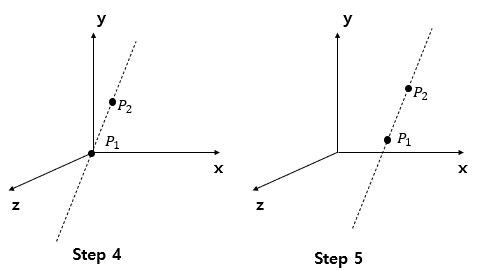
Step1~5 까지 머릿속으로 하는 건 쉽다.
그런데 Step2 에서 z축에 맞게 회전은 어떻게 시켜주는지 한번에 머릿속에 그려지지 않는다.
z축에 맞게 어떻게 회전시켜줄까?

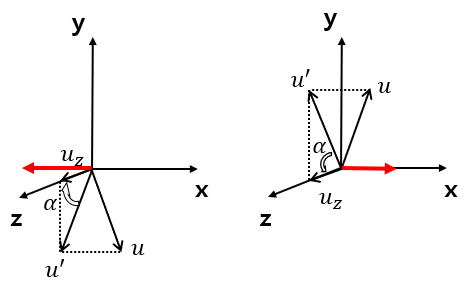
P2 - P1 vector를 u라고 해보자.
순서는 이와 같다.
Step 2의 Step1. x축 중심으로 α만큼 회전해서 xz평면으로 옮기기
Step 2의 Step2. y축 중심으로 β만큼 회전해서 z축에 맞춰주기

Step2의 Step 1의 α 구하기
여기서 Step 1의 α를 구하는 건 다음과 같다.

u를 yz평면에 정사영시키면 u' 벡터가 나오고,
이 u'과 uz 벡터 사이의 각도가 α이다.
그렇다는 건, u'과 uz를 dot product하면 α를 구할 수 있는 것이다.

u'과 uz 를 내적한 값(위 식의 분자부분)은 u'의 z값인 c 가 나오게 된다.
그리고 u'의 크기를 d라고 하고, uz의 크기는 1이다.
그리고 u'의 크기인 d는 피타고라스의 법칙으로 구할 수 있다.
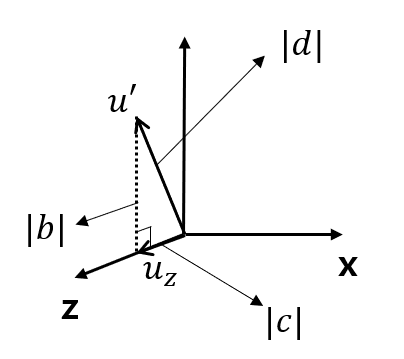

그래서 α를 다음과 같이 나타낼 수 있다.
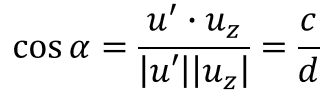
그런데 한가지 문제점이 있다.
벡터 u가 반대편에 위치한다면???

이러면 똑같은 α가 구해지게 된다.
이 때 문제점은 α를 +만큼 더해주냐, -만큼 더해주냐를 모른다는 것이다.
왜냐하면 cosα 값만 보고 어느방향인지 알 수가 없다.
따라서 어느 방향으로 돌려야 하는지를 알아내야 한다.
방향을 알기 위해서 cross product를 사용하자.

u' 과 uz를 cross product를 해서,
왼쪽 방향이 나오면 -α 만큼 회전하고
오른쪽 방향이 나오면 α 만큼 회전시켜주면 된다.
이것을 수식으로 풀어보자.

이 수식은 말로 해보면 ux는 방향이고, |u'||uz|sinα 는 크기이다.
이 때, sinα가 음수면 ux의 음수방향이고,
sinα가 양수면 ux의 양수방향이라는 뜻이다.
그런데 여기서 다음과 같이 b를 나타낼 수 있다.
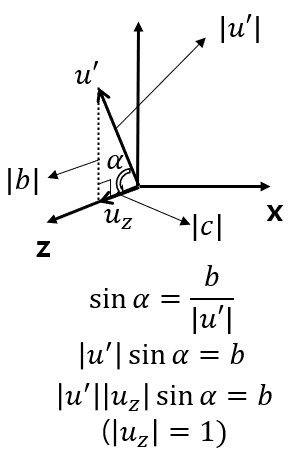
여기서 sinα 에 대한 식으로 나타내면 다음과 같다.

(참고)
sin이 양수면 위, 음수면 아래이다.
그래서 u의 y좌표인 b를 보면 위에 있는지 아래에 있는지 쉽게 알 수 있다.
중간 정리
이 때까지 구한 건 뭘까?

바로 cosα 와 sinα 를 구했다.
각도를 알기 위해 cos을 구했었고, 방향을 알기 위해 sin을 구했었다.
실제로 하는 계산
cos 과 sin을 알면? tan 를 구할 수 있다.

arctan 를 구하면, 부호를 고려한 α 값이 나오게 된다.
그래서 실제 연산할 때, arctan 를 많이 쓰기도 한다.
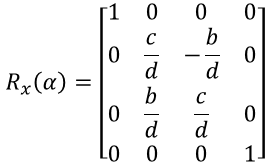
회전 matrix는 이와 같다.
Step 2의 Step 2의 β 구하기
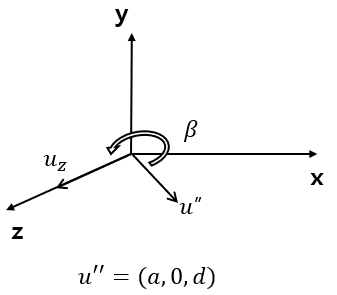
α 구할 때와 똑같이, u'' 과 uz를 dot product 해서 β를 구해보자.
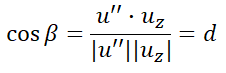
마찬가지로 u'' 과 uz를 cross product를 해서 방향을 구하자.

그러므로 sin을 구해보면 다음과 같다.
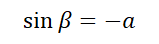
그래서 이제 cos 알고 sin 알고 있으니, tan로 해보자.
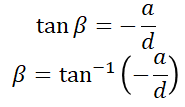
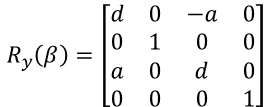
회전 matrix는 이와 같다.
중간 정리 2
좌표축과 평행하지 않는 임의의 축에 대해 θ만큼 회전할 때 연산은 다음과 같다.

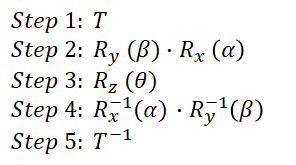
●Feedback
각도를 계산할 때 : dot product -> cos
방향을 알아볼 때 : cross product -> sin
이렇게 얻은 cos 과 sin 으로 tan를 구하고,
arctan로 부호를 고려한 각도를 구할 수 있다.
다른 형태의 matrix
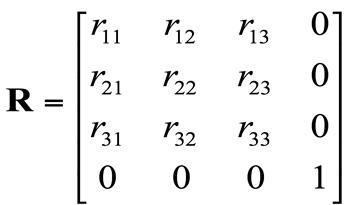
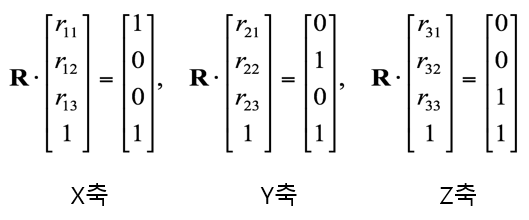
R의 첫번째 행을 R로 보내봤더니 x축이 span(생성)된다.
R의 첫번째 행 (r11, r12, r13) 은 x축 vector space를 span 하는 basis가 된다.
y축은 두번째 행, z축은 세번째 행에 속한다.
다시 말하면,
(r11, r12, r13)라는 vector를 R로 회전시키면, x축이 나온다는 것이다.
(r21, r22, r23) 을 R로 회전시키면 y축이 나온다.
(r31, r32, r33) 을 R로 회전시키면 z축이 나온다.
더 살펴보자.
지금부터 할 작업은
임의의 세 좌표축을 x, y, z 좌표축으로 회전시키는 작업을 할 것이다.


uz' 은 아까 u와 같고,
uy' 은 좌표축의 y축과 같이 만들려면, 길이는 1이어야 하고 방향은 x축과 z축에 수직인 방향이고,
ux' 은 좌표축의 x축과 같이 만들려면, uy'와 uz'에 수직이어야 한다.
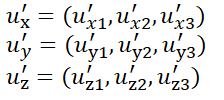
각 축의 요소들은 이러하다고 하자.
여기서 중요한 것은
uz' 과 uy' 과 ux' 은 서로 수직이고 크기가 1이라는 것이다.
이 벡터들을 행렬에 넣으면 회전행렬이 된다.
그 회전행렬은 아래와 같다.
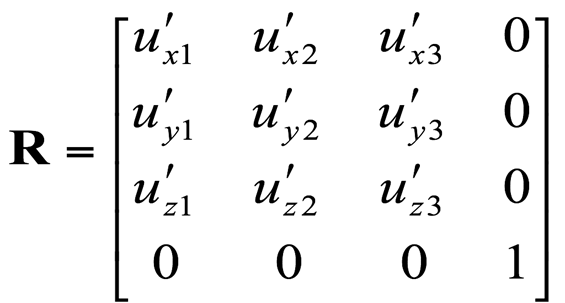
왜 회전행렬이 될까?
회전행렬의 특징에 따르기 때문이다.
1. 각 축들은 서로 수직이여야 한다.
2. 각 축들은 길이가 1이어야 한다.
그렇다면 이렇게 나온 R은 대체 무엇을 하는 걸까??

이전에 했던 Step 2에서 임의의 축을 진짜 z축으로 회전시키는 것과 똑같은 회전을 하고 있다.
좀 더 자세히 말하면
임의의 좌표축의 방향을 uz축이라고 잡고,
이 uz축에 대한 ux축과 uy축을 만들어주고,
이 축들을 회전행렬로 계산하면 진짜 x, y, z축 좌표계가 되는 것이다.
[참고]
Interactive Computer Graphics: A Top-Down Approach with Shader-based OpenGL 6th edition / 저자: Edward Angel, Dave Shreiner / 출판사: Pearson Education
'IT > 컴퓨터 그래픽스' 카테고리의 다른 글
| GPU와 Buffer (0) | 2021.01.17 |
|---|---|
| GPU에 data를 전달하기 (0) | 2021.01.17 |
| 3D Geometric Transformation (0) | 2020.12.04 |
| Homogeneous Coordinate (0) | 2020.12.04 |
| 2D Geometric Transformation (0) | 2020.12.04 |




댓글