2D Geometric Transformation
2D Geometric Transformation
순서
1. 2D Translation matrix
2. 2D Rotation matrix
3. 2D Scaling matirx
4. 실제 사용하는 matrix일까?
Transformation
만들어진 기하학적 물체의 위치를 바꾸거나, 방향을 바꾸거나, 종횡비를 바꾸거나, 크기를 바꾸거나 이런 변환 작업을 Geometric Transformation이라고 한다.
결국엔, 물체를 어디선가 만들었는데, 디스플레이 화면 상에 어디에 보여야할지의 문제라고 생각하면 된다.
우리 화면 상에 실제로 어디에 배치되어야 하냐는 것이다.
Transformation의 하나의 예시
Maya, 3D Max, Blender 등에서 어떤 물체를 만들었는데, 이것을 Unity, Unreal 등에 가져온다고 생각해보자.
이것은, 모델링 한 것을 실제 공간에 물체를 배치하는 것이다.
1. 물체를 만들 때의 좌표축 (Modeling Coordinates)
2. 화면 상의 좌표축 (World Coordinates)
이렇게 크게 두가지의 좌표축이 있다.
모델링을 하는 곳은 Modeling Coordinates를 사용하고,
실제 물체를 두는 공간에선 World Coordinates를 사용한다.
그래서 Modeling Coordinates에서 World Coordinates로 보내는 과정도 Transform이라고 할 수 있다.
Transform에는 크게 3가지가 있다.
1. Translation (이동)
2. Rotation (회전)
3. Scaling (크기변환)
우선 2D부터 살펴보도록 하자.
1. 2D Translation
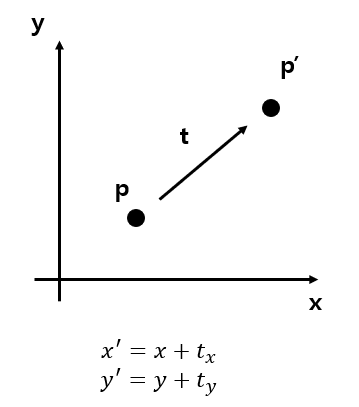
점 p에서 p' 으로 이동시켜본다고 하자. 그렇다면 어떤 행렬을 쓸까?
(실제론 이렇게 안하지만 비교를 위해 일단 사용해봄)

Translation matrix t는 이렇게 2 X 1 matrix로 표현된다.
2. 2D Rotation

어떤 물체 혹은 점을 회전시켜보자. 어떤 행렬을 쓸까?

Rotation Matrix R는 2 X 2 matrix로 표현된다.
여기서 주목할 만한 것은, 만약 회전하는 중심점이 원점이 아니라면, 원점으로 이동시키고 회전시켜줘야 한다.
그래서 회전하는 점의 식은 다음과 같다.

여기서 t는 원점으로 이동하는 translation matirx이다.
3. 2D Scaling

Scaling은 다음과 같은 행렬을 사용한다.
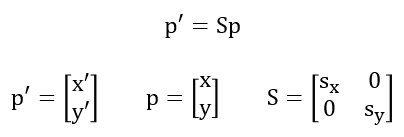
Scaling matrix는 2 X 2 matrix로 표현된다.
Scaling도 Rotation과 마찬가지로, 원점이 아니라면 원점으로 이동시키고 크기조절을 해줘야한다.
회전하는 점도 다음과 같다.

여기서도 t는 원점으로 이동시키는 translation matrix이다.
실제 사용하는 Matrix
정리해보자면,
translation matrix = 2 X 1 matrix
rotation matrix = 2 X 2 matrix
scaling matrix = 2 X 2 matirx
이렇게 말할 수 있다.
그러면 과연 실제로도 이렇게 계산되어질까?
실제 2D좌표의 세 개의 transformation matrix는 모두 3 X 3 matrix가 사용된다.
세 개의 matrix는 2차원 좌표계에다가, translation matrix는 형태도 달랐는데 어떻게 모두 3 X 3 matrix를 사용할까?
바로 Homogeneous Coordinates를 사용하는 것이다.
내용은 다음 글 Homogeneous Coordinates와 이어짐
[참고]
Interactive Computer Graphics: A Top-Down Approach with Shader-based OpenGL 6th edition / 저자: Edward Angel, Dave Shreiner / 출판사: Pearson Education